Methode
De Normaal
Het KNMI heeft in 2020 een standaard methode voorgesteld voor het bepalen van een trend voor communicatie buiten onderzoeksrapporten en wetenschappelijke publicaties om. Dit rapport is via deze link te lezen: https://cdn.knmi.nl/system/ckeditor_assets/attachments/161/TR389.pdf
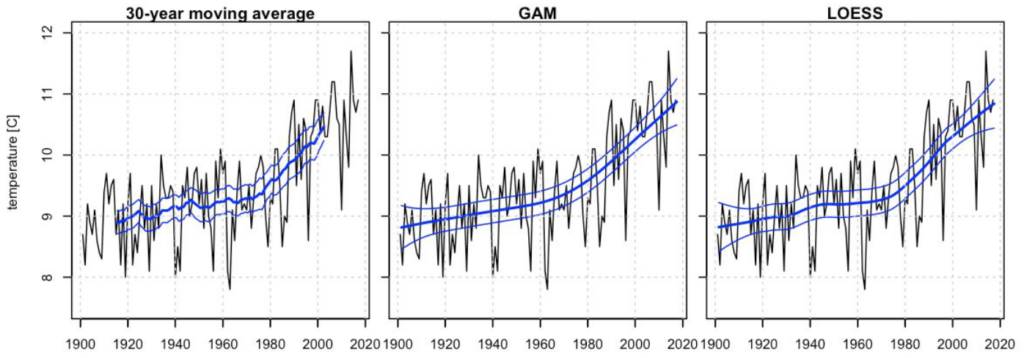
In dit document van het KNMI wordt de LOESS (locally estimated scatterplot smoothing) methode, met een periode van 42 jaar, gekozen als meest accurate methode voor het beschrijven van een trend van weergegevens.
De LOESS waarde is volgens deze criteria voor alle datapunten berekend en wordt hier op deze site verder de normaal genoemd. Deze normaal wordt op de grafieken samen met de datapunten getekend.
Classificatie
Om een periode te kunnen beschrijven als warm, zeer nat of extreem zonnig, zijn objectieve criteria nodig. Deze criteria bestaan hier uit twee delen; de afwijking vanaf de normaal en de extreemheid van deze afwijking.
De afwijking vanaf de normaal wordt voor ieder datapunt bepaald over dezelfde periode als de normaal. Dit wordt gedaan door de standaardafwijking te bepalen ten opzichte van de normaal. Door de aard van de berekening van de standaardafwijking en het beperkte aantal datapunten wordt een springerig karakter behouden. Hierom wordt een LOESS waarde van deze standaardafwijking bepaald zodat er een lokaal representatieve waarde van de standaardawijking voor ieder datapunt verkregen wordt. Ieder datapunt krijgt hierdoor een afwijking van de normaal van een x-aantal standaardafwijkingen, die hier de aberratie genoemd zal worden. Aberratie is wellicht geen gebruikelijk woord voor zoiets, maar er moet ook voorkomen worden dat duidelijk gedefinieerde woorden uit bijvoorbeeld de statistiek nieuwe betekenissen krijgen voor allerlei toepassingen.
Bepaling van classificaties
Om te bepalen wat extremen zijn, is er een arbitraire keuze nodig. Hier is gekozen om 50% van de datapunten, gesorteerd naar aberraties, als normaal te beschouwen. Dit is een lager percentage dan wat zou volgen uit de normaalverdeling (~68.2%), maar laat daarom meer ruimte voor het behouden van 3 verschillende classificaties buiten de normale bandbreedte. De keuze om de helft van de datapunten als normaal te beschouwen betekent vervolgens dat elk 25% van de waarden aan de hoge kant of lage kant van normaal horen.
Om dit verder te differentiëren naar de 3 reeds gebruikte classificaties, ‘hoog’, ‘zeer hoog’ en ‘extreem hoog’ (evenzo voor laag), is hier bepaald dat het aantal datapunten dat binnen ‘zeer hoog’ valt, 50% van de datapunten moet zijn dat binnen ‘hoog’ valt en dat het aantal datapunten dat binnen ‘extreem hoog’ valt, 50% van de datapunten moet zijn dat binnen ‘zeer hoog’ valt. Dit leidt tot de onderstaande verdeling:
| extreem hoog | ~3.6% |
| zeer hoog | ~7.1% |
| hoog | ~14.3% |
| normaal | 50.0% |
| laag | ~14.3% |
| zeer laag | ~7.1% |
| extreem laag | ~3.6% |
Deze classificaties worden als grenswaarden op de grafieken getekend en vormen de ondergrens voor deze classificaties, gezien vanaf de normaal. Met een dataset van rond de 120 jaar voor de Bilt, betekent dit dat elke extreme afwijking van de normaal gedurende een periode 4 keer voorgekomen is, ruwweg eens in een generatie.
Nadelen
Zoals beschreven in het rapport van het KNMI, zijn er een aantal nadelen bij het gebruik van de LOESS methode:
- Hogere onzekerheid bij het begin en eind van de dataserie wegens een verminderd aantal datapunten
- Recente waarden zijn niet in beton gegoten tot de helft van de beoordelingsperiode (21 jaar) gepasseerd is
- De LOESS-waarde is niet simpel uit te rekenen met een rekenmachine of speadsheet
Deze punten moeten wel afgewogen worden tegenover wat zou gelden voor de gangbare methode van ’30-jaar lopend gemiddelde’ om een gebalanceerd beeld te creëren:
- Geen normaal vast te stellen voor de eerste 30 jaar uit de dataserie
- Recente waarden zijn definitief, maar lopen in een sterk veranderend klimaat een halve beoordelingsperiode (15 jaar) achter op de realiteit
- Simpel uit te rekenen, maar levert springerige data op die sterk beinvloedt wordt door extreme individuele datapunten. De lijn kan zomaar een sprong maken omdat een extreem datapunt van 30 jaar geleden uit de reeks verdwijnt
Verbeteringen
Voor alle tips of aanwijzingen om deze methode te verbeteren, kunt u hieronder een berichtje sturen.